Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo Exercícios Adicionais.6 - Ex. 146

Seja o Δ A B C com A   = ( 2,0 , - 4 ) , B   = ( 4,4 , 4 ) e C   = ( - 6,4 , 8 ) . Determine o ponto de encontro de duas medianas e demonstre que a terceira mediana também passa por esse ponto.

Passo 1

Galera, antes de começar, vamos relembrar o conceito de mediana. Mediana é a reta que sai de um vértice e vai até o ponto médio oposto a esse vértice. Se M , N , P são os pontos médios de A B ̄ ,   B C ̄ , A C ̄ , respectivamente, então, temos as seguintes relações (esse resultado foi mostrado no Exercício Resolvido 3, você pode dar uma olhadinha lá)

C M → = 1 2 ( C A → + C B → ) = - 1 2 ( A C → + B C → ) = - 1 2 ( A C → + B A → + A C → ) = - A C → + 1 2 A B →

A N → = 1 2 ( A B → + A C → )

B P → = 1 2 ( B A → + B C → ) = 1 2 ( - A B → + B A → + A C → ) = - A B → + 1 2 A C →

Também deixamos uma figura para ajudar no entendimento.

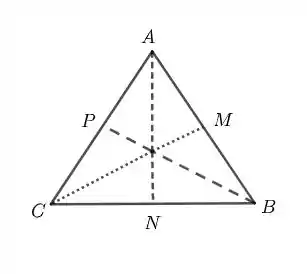
Passo 2

Vamos supor que as duas medianas C M → e A N → se encontrem num ponto Q . Então, temos

C Q → = α C M → = α ( - A C → + 1 2 A B → )

A Q → = β A N → = β 2 ( A B → + A C → )

Mas, temos uma trajetória alternativa entre A e Q :

A Q → = A C → + C Q → = A C → + α ( - A C → + 1 2 A B → )

As duas expressões que obtivemos para A Q → são equivalente, ou seja,

β 2 ( A B → + A C → ) = A C → + α ( - A C → + 1 2 A B → )

⇒ β 2 - α 2 A B → = 1 - β 2 - α A C →

Os vetores A B → e A C → claramente não são paralelos. Então, só tem um jeito da igualdade acima ser verdadeira:

β 2 - α 2 = 0 ⇒ α = β

1 - β 2 - α = 0 ⇒ 1 - β 2 - β = 0 ⇒ 3 2 β = 1 ⇒ β = α = 2 3

Assim, as duas medianas se interceptam em ponto Q e temos

C Q → = 2 3 ( - A C → + 1 2 A B → )

A Q → = 1 3 ( A B → + A C → )

Passo 3

Só falta a gente mostrar que a terceira mediana também passa por esse ponto. Para isso, temos que mostrar que o vetor B Q → = γ B P → . Já calculamos B P → = - A B → + 1 2 A C → lá no Passo 1, agora falta B Q → :

B Q → = B A → + A Q → = - A B → + A Q → = - A B → + 1 3 ( A B → + A C → ) = - 2 3 A B → + 1 3 A C → = 2 3 ( - A B → + 1 2 A C → )

B Q → = 2 3 B P →

Viram o que a gente fez? Mostramos que B Q → = γ B P → com γ = 2 3 . O ponto de encontro das medianas tem um nome especial, baricentro, e fica localizado exatamente a dois terços do trajeto entre o vértice e o ponto médio oposto. Por isso, nós obtivemos α = β = γ = 2 3 .

E aí, gostou desta resolução? Responde Aí!

Resposta

Veja a resolução acima.