Seja munido da operação dada pela seguinte tábua:
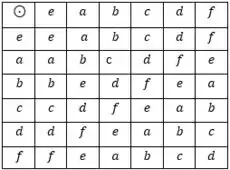
a) admitindo a propriedade associativa prove que é um grupo não comutativo.
b) Obtenha os subgrupos de E com ordem .
Passo 1
Fala aiii meus lindos tudo blz? espero que sim
Então se liga só nessa questão do livro de álgebra moderna do Gerson Iezzi seja munido da operação dada pela seguinte tábua:
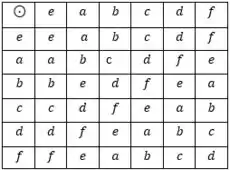
a) admitindo a propriedade associativa prove que é um grupo não comutativo.
b) Obtenha os subgrupos de E com ordem .

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Na letra (a) para provar que é um grupo comutativa temos que,
É comutativo
Já na letra (b) para se obter os subgrupos de com ordem , temos
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.

Resposta
a) É comutativo.
b)