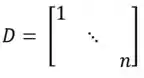Seja uma base de e , com k=1, ..., n.
b) Determine esta matriz diagonal
Passo 1
Para resolvermos essa questão de uma forma bem facinha, basta lembrar as condições que tornam uma matriz diagonalizável se existe P invertível tal que com D diagonal.
Portanto, pode ser escrito como as colunas de P são autovetores de A com autovalores k na diagonal de D. Essa questão específica pede que escrevemos a matriz diagonal, no caso se refere a matriz D, até aqui beleza, né? Então, nós sabemos que os autovalores de D são k e, de acordo com o comando, k=1, ..., n. Logo a matriz D, pode ser escrita como:
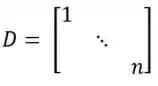
E aí, vamos destruir a próxima questão também?
Resposta