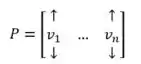Seja uma base de e , com k=1, ..., n.
- Mostre que existe P tal que é diagonal;
Passo 1
Para resolvermos essa questão de uma forma bem facinha, basta lembrar as condições que tornam uma matriz diagonalizável se existe P invertível tal que com D diagonal.
Portanto, pode ser escrito como as colunas de P são autovetores de A com autovalores k na diagonal de D. Para isso, P necessariamente teria que ser escrito com cada coluna um autovetor , a questão nos disse que , logo, que seja diagonalizável, P deve ser:
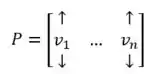
E prontinho, terminamos, topa resolvermos outra questão juntos?
Resposta