Seja P o pé da perpendicular baixada do foco F da hipérbole
A uma das assíntotas. Demonstre que onde O é a origem do sistema de coordenadas
Passo 1
Primeiro vamos usar um desenho para ajudar
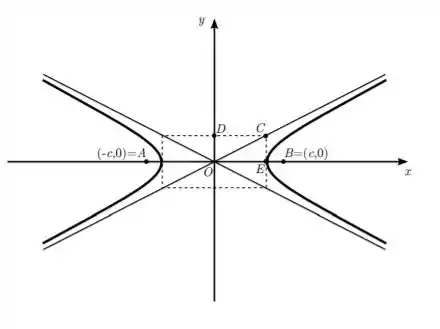
Esse desenho nos ajuda a entender o que está ocorrendo, pois temos esse retângulo no meio.
A altura do retângulo é 2b e sua largura é 2a.
Agora olhe para o ponto C, temos que sua distância até a origem é maior que a, pois ele é hipotenusa de um triangulo com um dos catetos medindo a. Como queremos um ponto P, onde sua distância até a origem é a, já podemos pensar que esse ponto P é da mesma assíntota do ponto C, porém antes dele.
Passo 2
Vamos tomar agora a equação de uma das assíntotas, no caso a assíntota que contém o ponto C:
Agora nós temos uma outra reta que passa por P e por F e é perpendicular à assíntota.
Logo
Como F pertence à reta r e
Passo 3
Agora iremos usar a fórmula de distância entre ponto e reta:
Onde s é a assíntota.
Aplicando a fórmula:
A primeira parte já foi, agora vamos para segunda.
Agora poremos só aplicar o teorema de Pitágoras, pois de e
E sabemos que PFO é um triângulo retângulo, com hipotenusa FO:
Logo, pela relação base da hipérbole
Resposta
Demonstração