Seja a reta .
- Escreva equações paramétricas da reta .
- Verifique quais dos pontos , , e pertencem à reta e localize-os corretamente na reta . Dados:
- Determine em um ponto cujas coordenadas são todas números inteiros.
, , e .
Passo 1
- Para escrever as equações paramétricas da reta, temos que igualar as equações que temos a algum parâmetro:
- O que vamos fazer aqui é, basicamente, substituir cada ponto nas equações paramétricas de e encontrar qual valor de satisfaz a igualdade. Se tivermos o mesmo valor de para as três equações, então o ponto pertence à reta. Vamos lá, então?
Agora, resolvermos a equação acima para encontrar e , que já serão as equações paramétricas:
Ou seja,
Passo 2
- Ponto :
Todos os valores de foram iguais, então o ponto pertence à reta.
- Ponto :
O ponto também pertence à reta.
- Ponto :
Como encontramos dois valores diferentes de , então não pertence à reta.
- Ponto :
Obtivemos valores iguais de . Então também não pertence à reta.
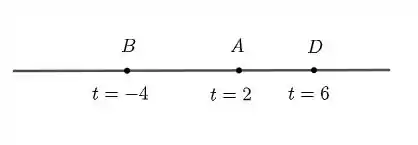
Resumindo, somente os pontos e pertencem à reta para , e , respectivamente. Você pode observar esses pontos na figura abaixo:
Passo 2
Para que seja inteiro, um valor possível de é . Nesse caso, . Agora, vamos substituir nas outras duas equações:
Com isso, chegamos no ponto que pertence a reta mas que só tem valores inteiros .
Resposta
- e pertencem a reta, não pertence.