Seja
- Encontre matrizes elementares tais que
é uma matriz triangular superior.
(b) Determine as inversas de = . Que tipo de matriz é L? Verifique que A = LU.
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
- Tenhamos
- O que nós temos
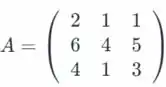
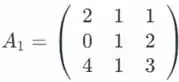
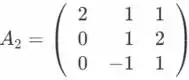
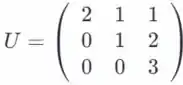
Considere as matrizes elementares
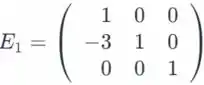
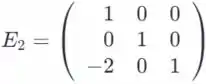
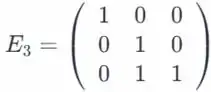
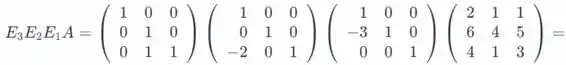
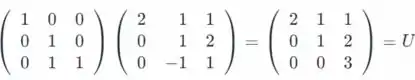
Passo 2

Então
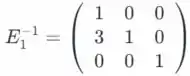
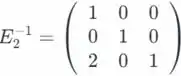
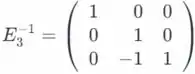
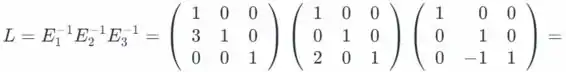
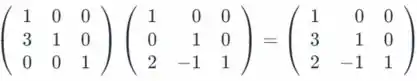
Nós temos que L é uma unidade de matriz triangular inferior.

Resposta
Resposta nos passos.