Sejam. Mostre que.
Passo 1
Vamos começar relembrando o que é produto vetorial!
O produto vetorial de é dado por :
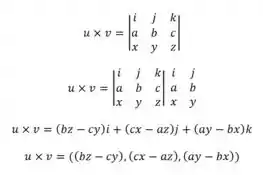
Então,
Passo 2
Então,
Passo 3
Então,
Resposta
Ei, a resposta está no passo a passo :)
Sejam. Mostre que.
Vamos começar relembrando o que é produto vetorial!
O produto vetorial de é dado por :
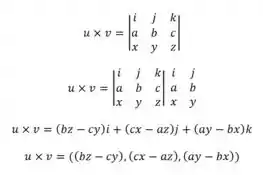
Então,
Então,
Então,
Ei, a resposta está no passo a passo :)