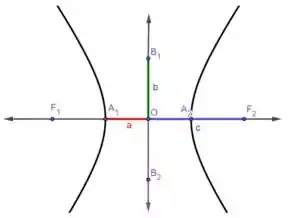
Sejam a e b números reais tais que e considere os pontos , e
- Mostre que as equações da elipse de vértice e focos e da parábola de vértice e foco podem ser escritas, respectivamente, nas formas
- Se os pontos pertencem, respectivamente, à elipse e à parábola do item a), mostre que
- A partir dos itens a) e b), conclua que a parábola de vértice e foco pode ser imaginada como a posição limite da elipse de vértices e focos quando o foco tende para o infinito.
Passo 1
Falaaaaa rapaziada tudo blz?
Nesta questão dado que a e b são números reais tais que e considerando os pontos , e e a partir daí encontrar
- Mostre que as equações da elipse de vértice e focos e da parábola de vértice e foco podem ser escritas, respectivamente, nas formas
- Se os pontos pertencem, respectivamente, à elipse e à parábola do item a), mostre que
- A partir dos itens a) e b), conclua que a parábola de vértice e foco pode ser imaginada como a posição limite da elipse de vértices e focos quando o foco tende para o infinito.

Calma meu camarada vamos solucionar ela juntos.
Passo 2
Na letra (a) a partir das definições da elipse e parábola vamos ter que,
Na letra (b) dado que
E na letra ( c ) o gráfico fica assim,
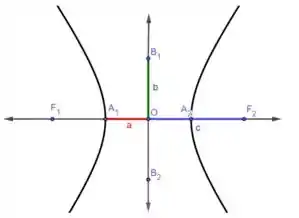
Resposta
a)
b)
c)