Sejam S e T TLs tais que façam sentido a composição ST. Mostre que:
(c) se ST é sobrejetiva, então S é sobrejetiva;
Passo 1
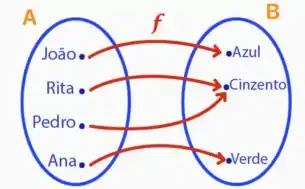
Um bom primeiro passo aqui é relembrar o conceito de sobrejetividade, de uma forma simples, cada um dos elementos pertencentes ao conjunto de chegada B, tem que estar ligado a um elemento do conjunto de partida A, assim como mostrado na imagem abaixo:
Passo 2
Usando esse conceito, nós vamos aplicar a afirmação de que ST é sobrejetora, portanto, dado um w qualquer, existe um y tal que . Se chamarmos Ty=v, então continuamos tendo , logo S também deve ser sobrejetiva!!
Prontinho, agora é só partir pro abraço 😊
Resposta
S é sobrejetiva.