Sejam S e T TLs tais que façam sentido a composição ST. Mostre que:
(d) se ST é injetiva, então T é injetiva;
Passo 1
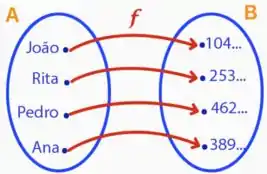
Um bom primeiro passo aqui é relembrar o conceito de sobrejetividade, de uma forma simples, objetos diferentes têm que ter imagens diferentes. Isto é, dois elementos do conjunto A, não podem estar ligados ao mesmo elemento do conjunto B, assim como mostrado na imagem abaixo:
Passo 2
Usando esse conceito, nós vamos aplicar a afirmação de que ST é injetiva, portanto, considerando uma transformação linear tal que , então , ah beleza mas e agora? É simples simples, a gente já sabe que ST é injetiva, logo, isso exige que v=w, portanto T é injetiva!!
Prontinho, agora é só partir pro abraço 😊
Resposta
T é injetiva.