Se a série é de termos positivos, determine se converge ou diverge; se a série contém termos negativos, determine se é absolutamente convergente, condicionalmente convergente ou divergente.
Passo 1
Eaew, tudo certinho?
Nesta série é conveniente analisarmos diretamente o teste do limite, o primeiro que aprendemos quando estamos analisando convergência de séries infinitas, ele diz o seguinte:
Se tivermos que , ou se L é indefinido, a série diverge. Se temos que , o teste é inconclusivo. Então, vamos verificar isto daqui.
Passo 2
Vamos calcular o limite que apresentei acima:
Podemos analisar o comportamento desta série, em termos de suas somas parciais, note que:
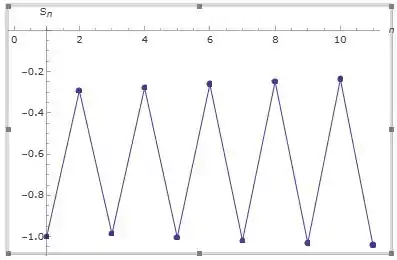
Esse comportamento se repete, o que indica que este limite é indeterminado, desta forma podemos afirmar a divergência da série. O comportamento das somas parciais pode ser observado no gráfico a seguir:
A questão foi isso! Te vejo na próxima! Tchauzinho!!
Passo 3
Reescrevendo a última igualdade do limite, temos:
Como , temos que essa série necessariamente diverge, é isso!! Te vejo na próxima! Tchau Tchau!