Para o sistema abaixo interprete cada equação como uma reta em , faça o gráfico e determine geometricamente o número de soluções:
Passo 1
Sejam e as retas dadas pelas equações e , respectivamente. Inicialmente, iremos determinar dois pontos de cada uma dessas retas para podermos desenha-las.
Zerando a variável na equação obtemos , de forma que o ponto pertence a reta . Agora, zerando a variável na mesma equação, obtemos , ou seja, é outro ponto de .
Usando a mesma estratégia na equação , obtemos os pontos e da reta .
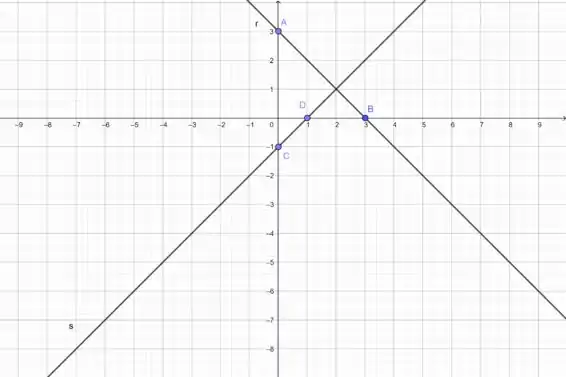
Tendo essas informações, podemos desenhar a figura abaixo:
Passo 2
Pela imagem, temos que as retas e se interceptam em um único ponto, donde concluímos que o nosso sistema linear possui uma única solução.
Resposta
O sistema linear possui uma única solução.