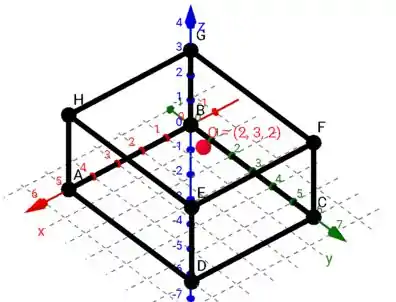
Um tanque de base retangular tem, em metros, as seguintes dimensões: base , altura . Dois terços do volume do tanque são ocupados por água. Na superfície superior da água forma-se uma pequena bolha de ar. A bolha está a igual distância das superfícies das paredes dede base e, em relação às paredes de de base, sua posição é tal, que a distância a uma das paredes é o dobro da distância à outra.Estabeleça um sistema de coordenadas, tendo como origem um dos cantos inferiores do tanque e como um dos planos de coordenadas a parede, de base, mais próxima da bolha, e dê, em relação a este sistema, as coordenadas do ponto onde se encontra a bolha.
Passo 1
Em primeiro lugar vamos estabelecer os vértices do tanque para o sistema de coordenadas:
Representamos a base como um retângulo de vértices - satisfazendo a condição da origem ser em um dos cantos inferiores do tanque- e e.
Além disso, os pontos E(5,6,3), F(0,6,3), G(0,0,3) e H(5,0,3) garantem uma altura igual a 3 para o tanque.
Com os vértices determinados, vamos representar no gráfico?!
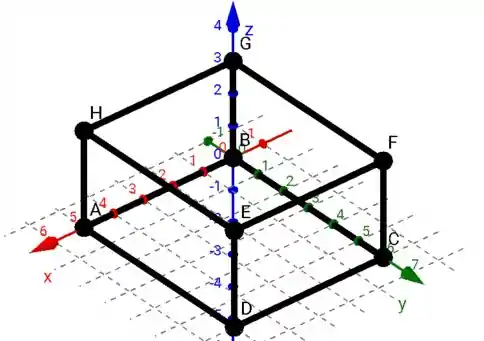
Passo 2
Mas, e a água?
Sabemos que o volume da água ocupa dois terços do tanque, que a área da base é a mesma para o volume do tanque e da água e que o volume é dado pelo produto de área da base e altura.
Então, , sendo o volume da caixa; a área da base e a altura da caixa.
E , sendo a altura da água.
Assim, . Com , temos .
Já encontramos a altura que a bolha está!
As coordenadas da bolha são: .
E as outras coordenadas da bolha?!
Passo 3
O exercício diz que a bolha está a uma mesma distância das paredes de , ou seja, está na metade do segmento entre as paredes. Sabemos a distância entre as paredes? Sim!! É justamente , que dividido por dois resulta em .
As coordenadas da bolha são:.
Agora só falta a coordenada x!
Em relação às paredes de 5 m, a distância da bolha a uma das paredes é o dobro da distância à outra. Ou seja, dividindo a distância entre as paredes por , ficamos com . Assim, a bolha está à de uma parede e de outra.
Finalmente:
As coordenadas da bolha são:
Resposta
As coordenadas da bolha são: