Trace o gráfico da equação.
Passo 1
Olááá, tudo bem??
Nessa questão vamos trabalhar com sistemas de coordenadas, retas e planos e antes de pôr as contas na ponta do lápis, vamos fazer uma rápida revisão sobre o assunto.
Um sistema de coordenadas é uma correspondência entre pares ordenados , que representam um ponto ou um intervalo, e pontos de um plano como mostra a figura abaixo que contém alguns exemplos.
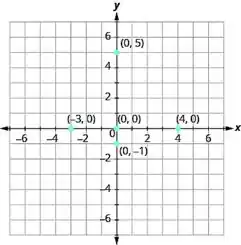
A partir destes pontos podemos esboçar retas, curvas e planos.
Passo 2
Agora que compreendemos as propriedades no Passo 1, vamos começar a resolução da questão.
A equação dada é não é linear porque o maior expoente de é e para esboçar o seu gráfico vamos primeiro encontrar os pontos críticos, ou seja, os pontos que interceptam o eixo e/ou o eixo . Quando
Logo,
A curva intercepta o eixo no ponto .
Passo 3
Agora vamos considerar
A curva intercepta o eixo no ponto .
Passo 4
O último passo é marcar os pontos no plano cartesiano e esboçar a curva. Como só temos dois pontos, vamos escolher valores aleatórios de , substituir na equação e encontrar o ponto .
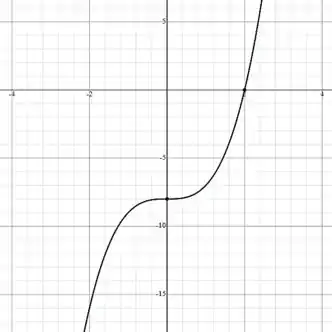
Até a próxima! =]