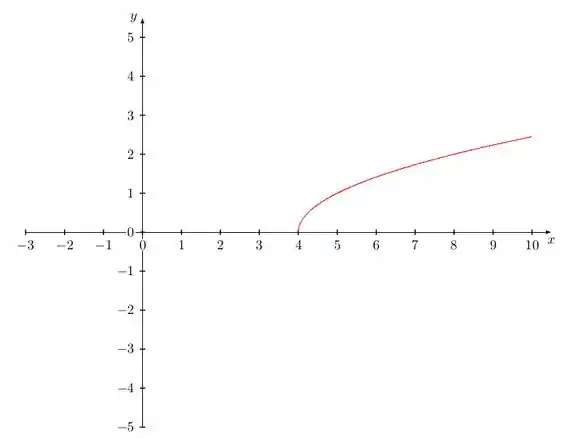
Trace o gráfico da equação.
Passo 1
Faaaaaaaaaaaaaala, pessoal! Tudo certinho? Vamos desenhar essa figura, explicando os principais passos utilizados na sua construção.
Passo 2
Sempre que temos um termo com raiz, como o que temos nessa questão, é interessante que nós a eliminemos. Como nossa raiz é quadrada, podemos eliminá-la elevando os dois termos ao quadrado. Isso nos dá
Isolando a variável , vamos obter
Essa é a equação de uma parábola, mas com a concavidade num sentido não convencional, ou seja, ela será para a direita. E ainda temos um “porém” aí nessa figura, porque a equação original envolve a raiz quadrada de um termo em , o que limita nosso domínio. Logo, teremos que desenhar uma “parábola deitada” que comece no ponto .
Eis a nossa parábola:
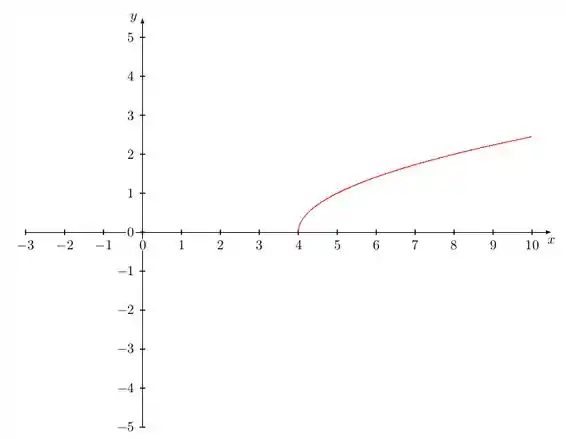
E assim, terminamos mais uma questão. Vamos pra próxima!
Resposta