Trace os gráficos das retas e determine seu ponto de intersecção.
Passo 1
Show de bola, galera! Vamos começar reescrevendo as equações. Isso vai nos permitir conhecer as características principais das retas e em seguida desenhá-las. Depois, vamos igualar as duas equações e encontrar o ponto de encontro.
Passo 2
A primeira equação pode ser escrita como
Trata-se de uma reta decrescente e que toca o eixo quando .
E a segunda equação pode ser escrita como
e se trata de uma reta crescente que toca o eixo quando .
Assim, o gráfico das duas retas é o representado abaixo:
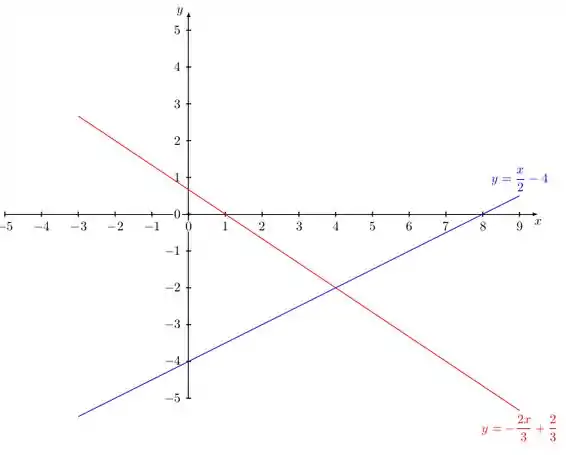
Passo 3
Vamos usar as duas equações e igualá-las:
Para encontrarmos o valor de , basta substituirmos o valor de encontrado em qualquer uma das equações. Vamos usar a primeira:
Logo, o ponto em questão é
E assim, finalizamos mais uma questão!
Resposta
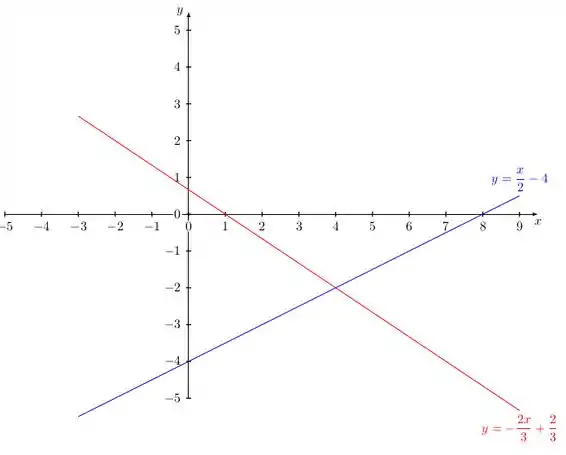
Ponto de intersecção: