é um trapézio, , , , e . Escreva em função de e .
Passo 1
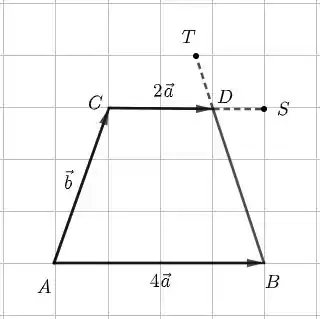
Galera, como temos um trapézio, dois dos lados são paralelos. Esses lados são e porque , . Outro detalhe que devemos ter atenção é que . Como os dois vetores têm a mesma origem, que é o ponto , então esse ponto está fora do trapézio. Já indica que está em algum ponto na direção de . Como ultrapassa o ponto , então também está fora do trapézio.
Além disso, como , então
e, também temos que
Passo 2
Também é conveniente escrever em termos de e . Para isso, temos que notar
Por outro lado, nós temos
Então, ficamos
Agora nós temos todos os ingredientes para obter :