No trapézio , temos: , e .
- Localize na figura os pontos e tais que e .
- Expresse como combinação linear de e .
Passo 1
Fala, pessoal! O trapézio dessa questão é mais ou menos assim:
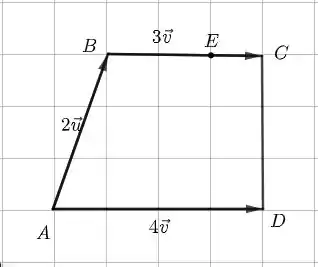
- Para localizar o ponto , que satisfaz , vamos usar
- Para expressar como combinação linear de e , temos que ir de a por um caminho alternativo:
Além disso,
Ou seja, o ponto está localizado a dois terços do segmento ligando a .
Nós vamos seguir mais ou menos o mesmo raciocínio e usar para determinar a localização de . Mas antes, temos que notar que essa relação indica que está no segmento . Temos
Assim, vemos que está a dois quintos do segmento .
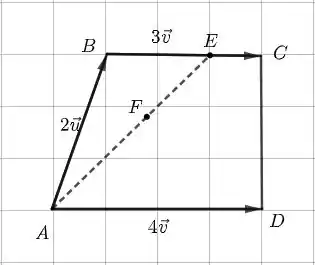
Passo 2
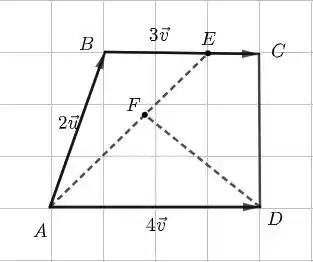
Agora, vamos expressar cada um desses vetores em termos de e :
Finalmente, podemos substituir esses resultados em