Em um triângulo , é ponto médio de , é ponto médio de , é tal que e é tal que . Demonstre, usando vetores, que e são colineares.
Passo 1
Fala, galera! Para provar que e são colineares, temos que mostrar que os vetores e são paralelos, porque isso garante que todos os pontos estejam numa mesma linha. Vamos começar desenhando o triângulos e todos os pontos:
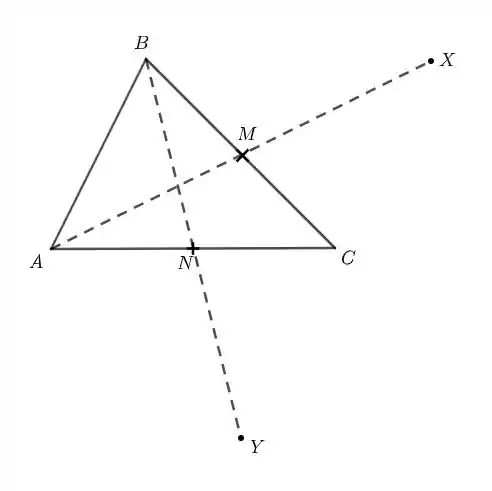
Como é ponto médio de e é ponto médio de , então podemos usar o resultado do Exercício Resolvido 3 do Capítulo 1 para escrever
Seria mais conveniente escrever todos os vetores em termos de dois dos vetores de vértice do triângulo, por exemplo, . Como , então
Passo 2
Agora, vamos usar as informações e :
Além disso,
Então
Como , então concluímos que e são colineares. Também podemos observar isso na figura:
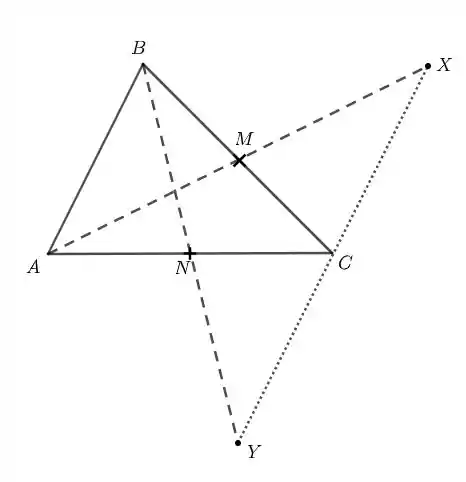
Resposta
Veja a resolução acima.