- Use a Definição (3.1) para obter o coeficiente angular da tangente ao gráfico da equação no ponto com coordenada -x. .
- Estabeleça a equação da tangente em .
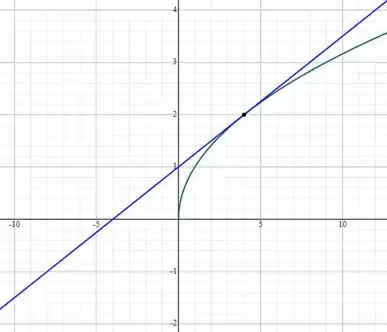
- Esboce o gráfico da curva e da tangente em .
Passo 1
Segundo a Definição (3.1), o coeficiente angular da tangente ao gráfico de uma função em é
Desde que o limite exista.
Se o limite na Definição (3.1) não existe, então o coeficiente angular da tangente em não é definido.
Esta é a definição formal da derivada da função no ponto . Ela representa o limite de uma sequência de coeficientes angulares de retas secantes que se aproximam da reta tangente em .
Passo 2
Compreendendo a Definição (3.1), vamos resolver a questão.
- Iremos substituir e na equação.
- Para encontrar a equação tangente no ponto , vamos substituir na equação do coeficiente angular
Observe que se substituirmos o valor de na equação, o denominador será igual a zero, logo temos o caso de um limite contendo indeterminação. Para resolver este limite, contornando a indeterminação, vamos recorrer ao par conjugado da expressão que conte a raiz (do numerador).
Eliminando os termos iguais,
Simplificando a equação,
Para finalizar a letra (a), vamos substituir o valor de na equação.
Passo 3
Agora para encontrar a equação da tangente vamos utilizar a equação fundamental da reta que possui o ponto e coeficiente angular igual a .
Substituindo os valores, temos que,
Passo 3
Para esboçar o gráfico da curva e da reta tangente em é só escolher alguns pontos em para encontrar valores em e assim traçar a curva que está representada abaixo:
Resposta