Use o MATLAB para resolver os Exercícios Numéricos.
Passo 1
Vamos fazer uso do pacote GAAL disponibilizado pelo próprio autor no livro. Iremos fazer a primeira de modo mais detalhado e as próximas sairão mais rapidamente. A primeira equação que iremos trabalhar é a do problema 6.3.1., dada por . Vamos declarar as nossas variáveis x e y e colocá-las num vetor que irá guardar o os seus valores
syms x y;
X=[x;y];
e também a matriz A dos coeficientes dos termos quadráticos
Passo 2
Uma vez declaradas os termos da nossa equação precisamos dizer também ao computador como é a nossa expressão, a equação da nossa cônica. Para isso:
esse termo acima nos diz que nossa equação é . Diagonalizando a matriz e montando a matriz com seus autovetores
[P,D]=diagonal(A)
Como precisaremos de um novo sistema de coordenadas , vamos declará-lo e colocar as informações num vetor
syms x1 y1;
X1=[x1;y1];
escrevendo a nossa equação em termos das novas variáveis
expr=subst(expr,X,P*X1)
simplificando (dividindo por 30, que é o termo livre de variáveis)
expr=expr/30
Passo 3
Realizando agora o plot do gráfico
elipse(sqrt(6),sqrt(3),P)
obtemos
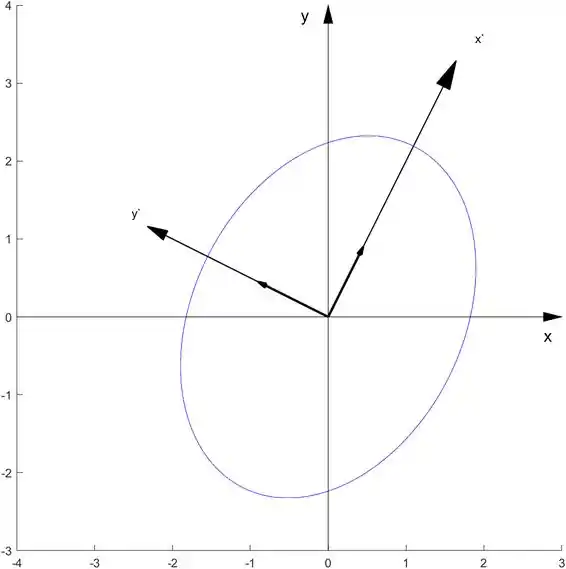
Passo 4
Agora que sabemos o processo para resolver, basta repetir para todas as outras equações.
Para o item 6.3.2.:
syms x y;
X=[x;y];
syms x1 y1;
X1=[x1;y1];
A=[3,-4;-4,-12];
expr=simplify(X.’*A*X+81)
[P,D]=diagonal(A)
expr=subst(expr,X,P*X1)
expr=expr/81
hiperbx(9/sqrt(13),9/2,P)
obtemos o seguinte plot
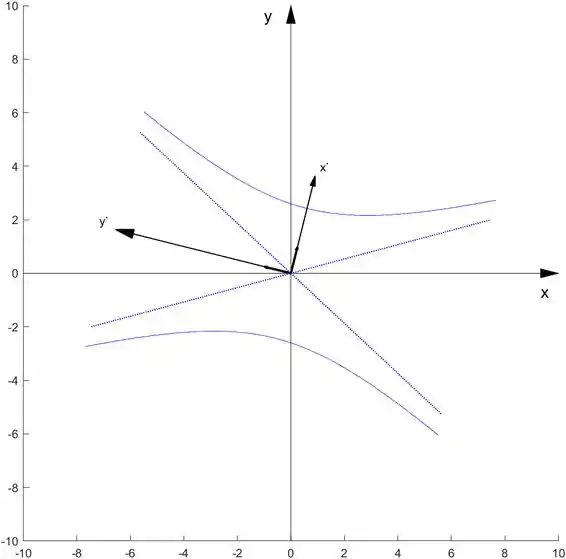
Para o item 6.3.3.:
syms x y;
X=[x;y];
syms x1 y1;
X1=[x1;y1];
A=[2,-2;-2,-1];
expr=simplify(X.'*A*X+24)
[P,D]=diagonal(A)
expr=subst(expr,X,P*X1)
expr=expr/24
hiperbx(sqrt(12),sqrt(8),P)
e recebemos
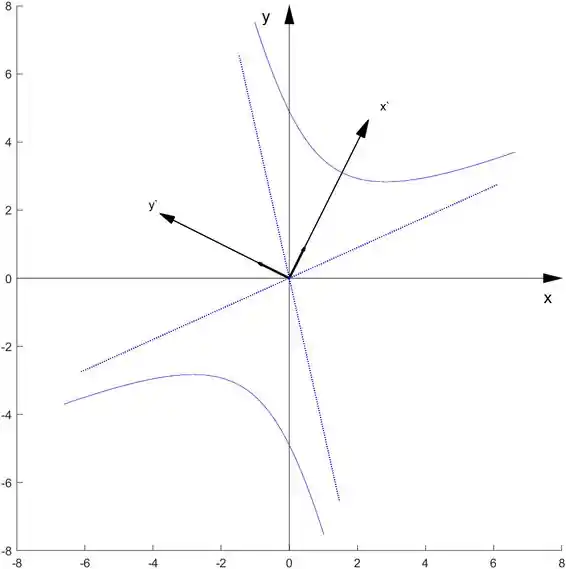
Para o item 6.3.4.:
syms x y;
X=[x;y];
syms x1 y1;
X1=[x1;y1];
A=[21,3;3,13];
expr=simplify(X.'*A*X-132)
[P,D]=diagonal(A)
expr=subst(expr,X,P*X1)
expr=expr/132
elipse(sqrt(11),sqrt(6),P)
e aparece na nossa tela:
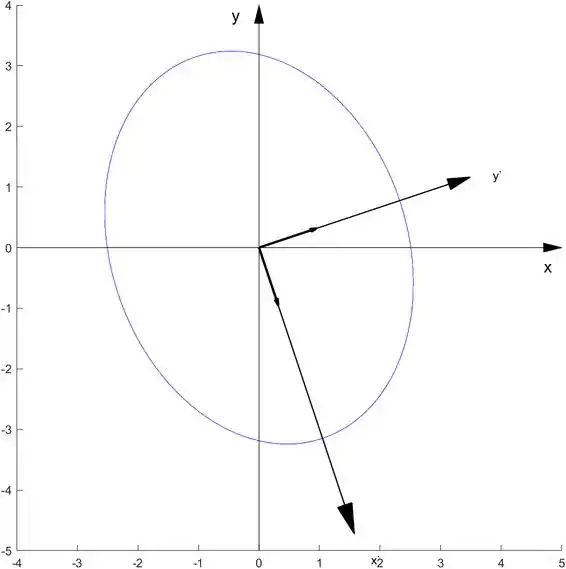
Para o item 6.3.5.:
syms x y;
X=[x;y];
syms x1 y1;
X1=[x1;y1];
A=[4,-10;-10,25];
K=[-15,-6];
expr=simplify(X.'*A*X+K*X)
[P,D]=diagonal(A)
expr=subst(expr,X,P*X1)
expr=expr/29
parabx(3/(4*sqrt(29)),P)
repare que também declaramos a matriz K, que nesse exemplo é não nula pois temos termos lineares nas variáveis x e y
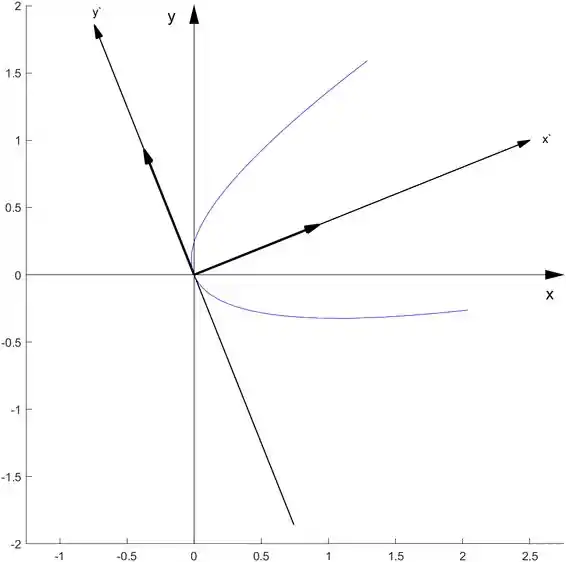
Para o item 6.3.6.:
syms x y;
X=[x;y];
syms x1 y1;
X1=[x1;y1];
syms x2 y2;
X2=[x2;y2];
A=[9,3;3,1];
K=[-10*10^(1/2),10*10^(1/2)];
expr=simplify(X.'*A*X+K*X+90)
[P,D]=diagonal(A)
expr=subst(expr,X,P*X1)
expr=subst(expr,y1,y2+1)
expr=subst(expr,x1,x2+2)
expr=expr/10
parabx(1,P,[2;1])
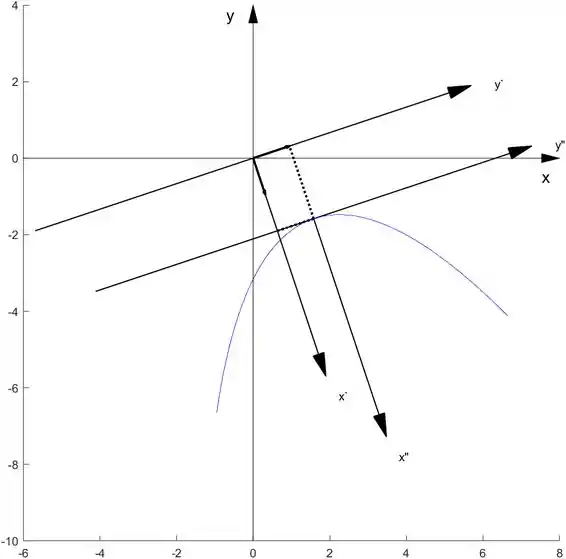
Para o item 6.3.7.:
syms x y;
X=[x;y];
syms x1 y1;
X1=[x1;y1];
syms x2 y2;
X2=[x2;y2];
A=[5,-3;-3,5];
K=[-30*(2)^(1/2),18*(2)^(1/2)];
expr=simplify(X.'*A*X+K*X+82)
[P,D]=diagonal(A)
expr=subst(expr,X,P*X1)
X0=[3;-3];
expr=subst(expr,X1,X2+X0)
expr=expr/8
elipse(2,1,P,X0)
o ponto em questão é o ponto que aparece ao completarmos o quadrado, na seguinte forma
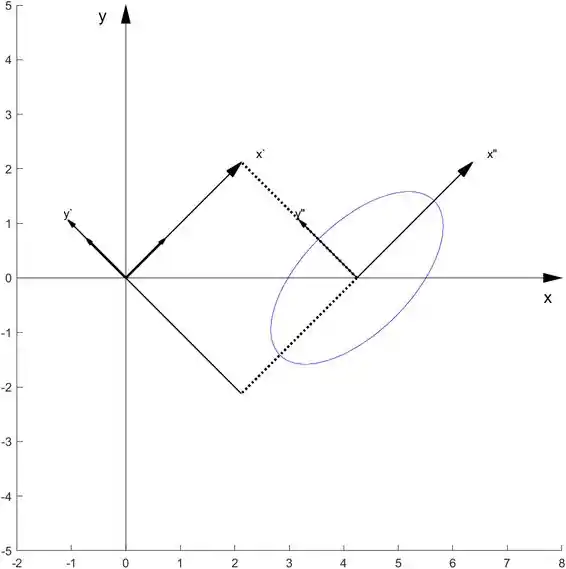
Para o item 6.3.8.:
syms x y;
X=[x;y];
syms x1 y1;
X1=[x1;y1];
syms x2 y2;
X2=[x2;y2];
A=[5,6;6,0];
K=[-12*(13)^(1/2),0];
expr=simplify(X.'*A*X+K*X-36)
[P,D]=diagonal(A)
expr=subst(expr,X,P*X1)
X0=[-3;2];
expr=subst(expr,X1,X2+X0)
expr=expr/36
hiperby(2,3,P,X0)
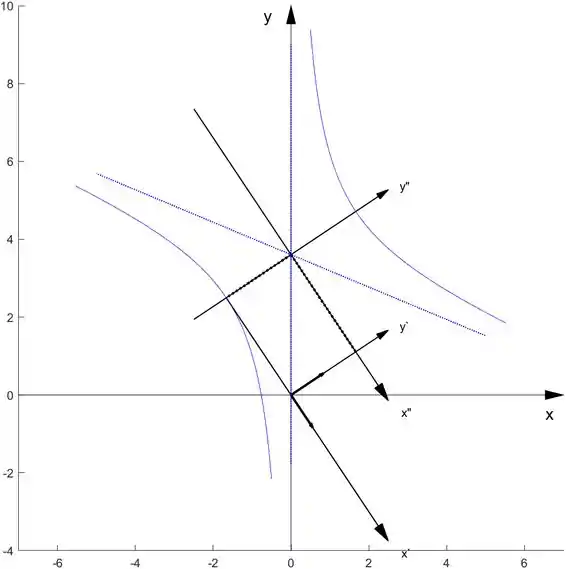
Para o item 6.3.9.:
syms x y;
X=[x;y];
syms x1 y1;
X1=[x1;y1];
syms x2 y2;
X2=[x2;y2];
A=[6,-2;-2,9];
K=[-4*5^(1/2),-18*5^(1/2)];
expr=simplify(X'*A*X+K*X-5)
[P,D]=diagonal(A)
expr=subst(expr,X,P*X1)
X0=[26/10;32/20];
expr=subst(expr,X1,X2+X0)
expr=expr*5/322
elipse(sqrt(322)/5,sqrt(161)/5,P,X0)
obtemos
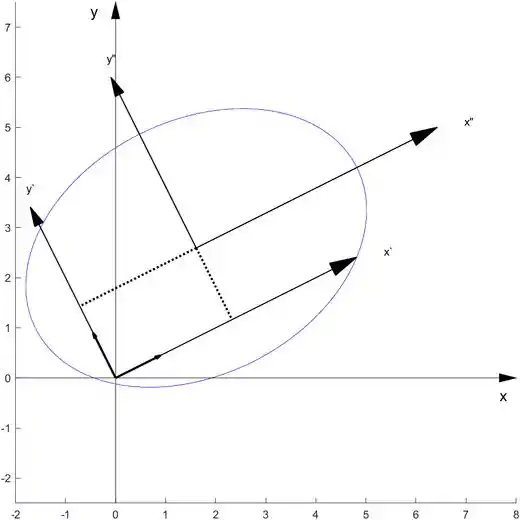
Para o item 6.3.10.:
syms x y;
X=[x;y];
syms x1 y1;
X1=[x1;y1];
syms x2 y2;
X2=[x2;y2];
A=[1,3^(1/2);3^(1/2),-1];
K=[6,0];
expr=simplify(X.'*A*X+K*X)
[P,D]=diagonal(A)
expr=subst(expr,X,P*X1)
X0=[-3*3^(1/2)/4;-3/4];
expr=subst(expr,X1,X2+X0)
expr=expr*4/9
hiperby(3/sqrt(8),3/sqrt(8),P,X0)
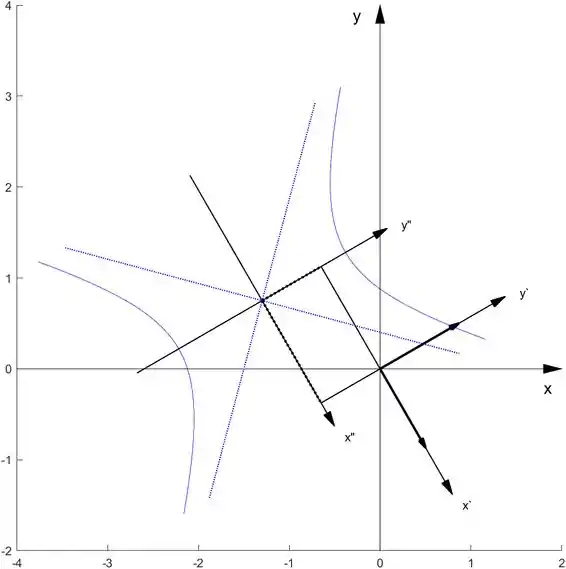
Para o item 6.3.11.:
syms x y;
X=[x;y];
syms x1 y1;
X1=[x1;y1];
syms x2 y2;
X2=[x2;y2];
A=[8,-8;-8,8];
K=[33*2^(1/2),-31*2^(1/2)];
expr=simplify(X.'*A*X+K*X+70)
[P,D]=diagonal(A)
expr=subst(expr,X,P*X1)
expr=subst(expr,y1,y2+2)
expr=subst(expr,x1,x2-3)
expr=expr/16
parabx(-1/32,P,[-3;2])
e aparece para nós
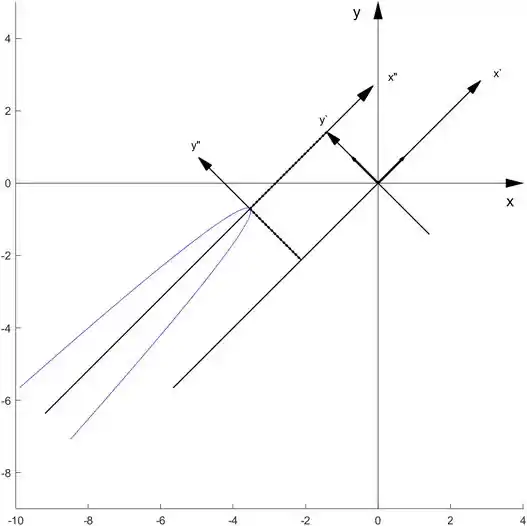
Para o item 6.3.12.:
syms x y;
X=[x;y];
syms x1 y1;
X1=[x1;y1];
syms x2 y2;
X2=[x2;y2];
A=[1,-3;-3,-7];
K=[10,2];
expr=simplify(X.'*A*X+K*X+9)
[P,D]=diagonal(A)
expr=subst(expr,X,P*X1)
X0=[1/10^(1/2);7/10^(1/2)];
expr=subst(expr,X1,X2+X0)
hiperby(4,1,P,X0, 'd')
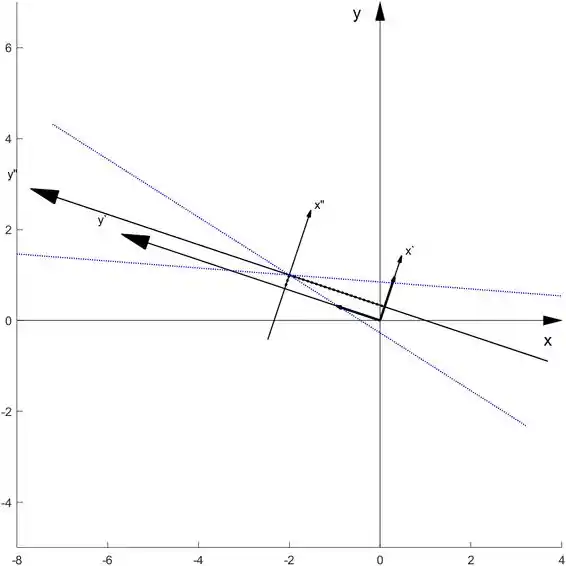
Ufa! Finalmente terminamos todas as cônicas.
Resposta
Ei, a resposta está no passo a passo :)