Vértice , foco .
Passo 1
Faaaaala, pessoal!!
Aqui ele pede pra gente achar a equação da parábola que verifica as condições dadas.
Primeiro vamos calcular o parâmetro desta parábola, onde é a distância entre o Foco e o Vértice.
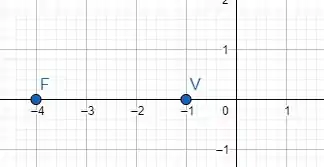
Analisando os pontos, podemos ver que a nossa parábola tem seu eixo em e está com sua concavidade virada para a esquerda. Logo, podemos dizer que .
Até aqui tá tranquilo, né?
Passo 2
Vamos observar uma coisa aqui: tivemos uma translação de eixos.
Nossa equação da parábola na forma padrão fica assim, pois como foi dito, o seu eixo é o eixo :
Onde temos
Podemos escrever a equação da nossa parábola da seguinte forma: