Vértice , simetria em relação ao eixo e passa pelo ponto .
Passo 1
Faaaaala, pessoal!!
Aqui ele pede pra gente achar a equação da parábola que verifica as condições dadas.
Primeiro, vamos verificar se o eixo da parábola pertence ao eixo ou . Essas são as informações que temos até o momento:
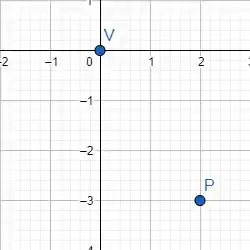
Como no enunciado diz que a parábola tem simetria ao eixo e seu vértice é , sabemos que ela pertence ao eixo . Isso implica que nossa equação será na forma:
Até aqui tá tranquilo, né?
Passo 2
Agora vamos pegar nosso ponto e substituir na equação para encontrar o valor de :
Logo, a nossa equação fica assim: