32. Mostre que, dado qualquer valor real de x,
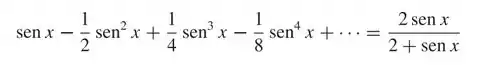
Passo 1
Oi oi, aluninho do Responde aí!
Para resolvermos essa questão, nós vamos relembrar o conceito de Séries Geométrica, nessa série cada termo é obtido multiplicando-se o termo precedente por alguma constante fixada. Assim, se o termo inicial da série for a e cada termo for obtido multiplicando-se o termo precedente por r , então a série terá a forma:

Passo 2
Olhando a série dada no comando percebemos que é uma série geométrica, será que é possível identificar o termo inicial e r que é a razão da série?
SIIIM, podemos considerar e . A partir desses termos nós podemos fazer uma análise de convergência, isso porque no teorema das séries geométrica temos que:
- se |r|
- se |r| ≥ 1 → Série Divergente
Como , então a série converge para todos os valores de x.
Passo 3
Sabendo que a série converge, utilizamos a propriedade de que a soma de séries é:
Logo, para qualquer valor de x, temos:
Resposta
Ei, a resposta está no passo a passo :)