a.Determine todos pontos x tais que f'x= 0
b.Analisar o sinal de f' e determinar os intervalos em que f é monótona
c.Analisar o sinal de f'' e determinar os intervalos em que f' é monótona
d.Traçar o gráfico de f.
Passo 1
a.Vamos derivar a equação para começarmos a resolver:
Ou seja:
b.Para analisar o sinal, basta olhar dentro dos parênteses:
Passo 2
c.Vamos derivar novamente para acharmos a segunda derivada:
Veja que , pois temos um valor positivo vezes outro valor sempre positivo, logo
Passo 3
d.
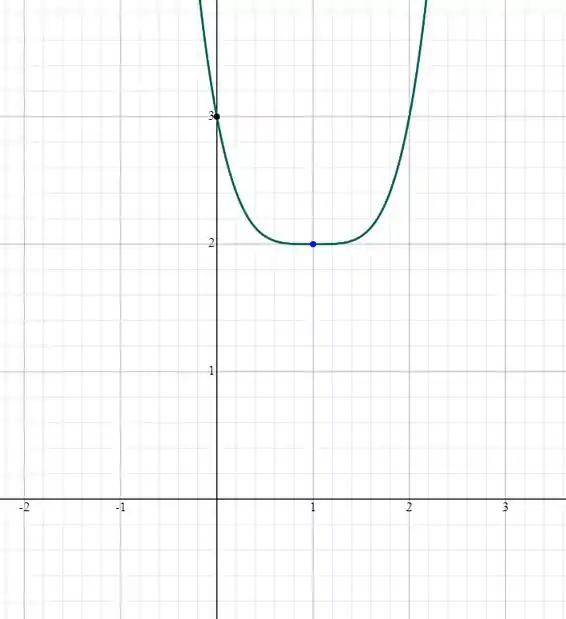
Resposta
a.
b.
c.