a.Determine todos pontos x tais que f'x= 0
b.Analisar o sinal de f' e determinar os intervalos em que f é monótona
c.Analisar o sinal de f'' e determinar os intervalos em que f' é monótona
d.Traçar o gráfico de f.
Passo 1
Para fazer o primeiro item vamos começar pela derivada de :
Igualando a zero achamos
Vamos agora para letra b, analisar o sinal de :
é uma parábola com concavidade para cima, como sabemos as raízes podemos afirmar que:
Nesse caso temos que é crescente
Além disso:
Nesse caso é decrescente
Passo 2
Para o item c vamos achar a segunda derivada:
Logo, para , no primeiro caso é crescente e no outro decrescente
Passo 3
O gráfico de f é:
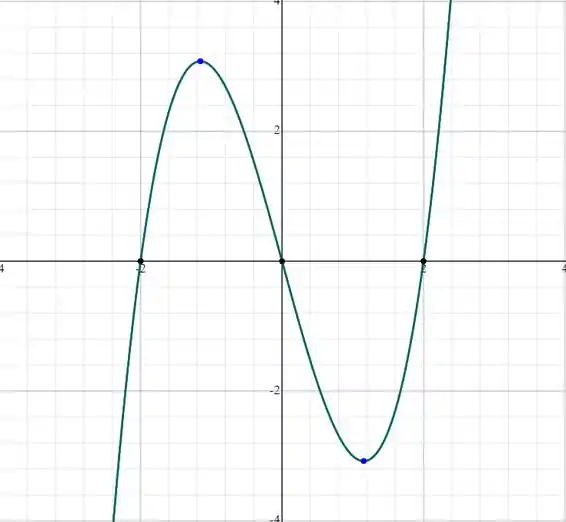
Resposta
a.
b.
c.