a.Determine todos pontos x tais que f'x= 0
b.Analisar o sinal de f' e determinar os intervalos em que f é monótona
c.Analisar o sinal de f'' e determinar os intervalos em que f' é monótona
d.Traçar o gráfico de f.
Passo 1
a.Vamos começar derivando a equação:
Temos que nunca será igual a zero
b.Para analisar o sinal basta olhar o denominador, pensando que é , assim será algo positivo sobre isso:
Passo 2
c.Vamos derivar novamente:
Ou seja,
Passo 3
d.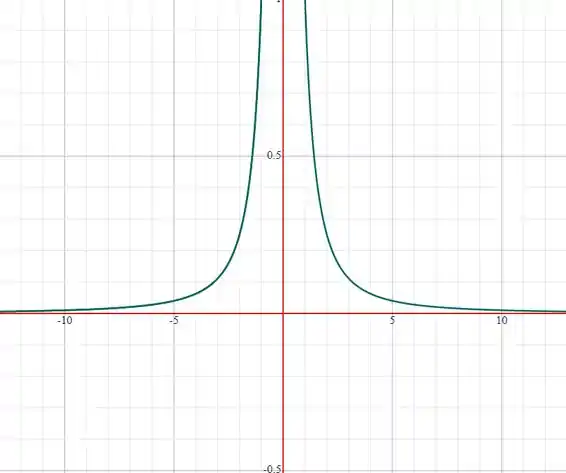
Resposta
a.
b.
c.