a.Determine todos pontos x tais que
b.Analisar o sinal de e determinar os intervalos em que f é monótona
c.Analisar o sinal de e determinar os intervalos em que é monótona
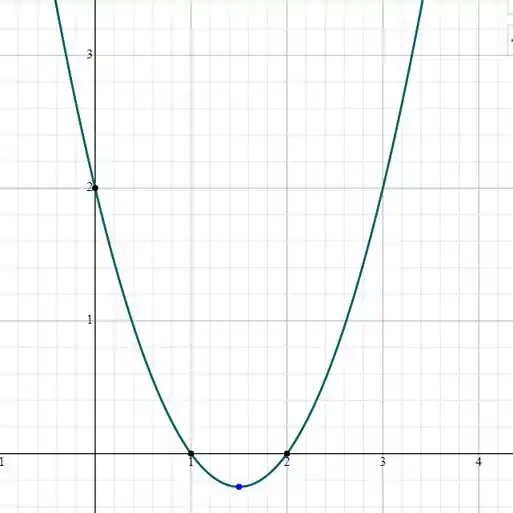
d.Traçar o gráfico de f.
Passo 1
Olharemos primeiro para o item (a):
Derivando a nossa equação, temos que:
Item (b):
Então:
Passo 2
Item c:
Derivando
Então é crescente para todo x.
Passo 3
Item (d):