Ângulos diretores e cossenos diretores
Os ângulos diretores α, β e γ de um vetor v = ai + bj + ck são definidos da seguinte forma:
α é o ângulo entre v e o eixo x positivo
β é o ângulo entre v e o eixo y positivo
γ é o ângulo entre v e o eixo z positivo
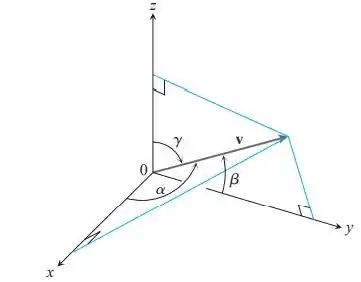
- Mostre que Esses cossenos são chamados cossenos diretores de v.
- Os vetores unitários são construídos a partir de cossenos diretores
Mostre que, se v = ai + bj + ck é um vetor unitário, então a, b e c são os cossenos diretores de v.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de produto escalar.
Vamos agora resolver os exercícios da seção 3 sobre ângulos entre vetores.
Item a
Inicialmente podemos escrever:
E:
Calculando o módulo de v:
Logo:
Passo 2
Item b
Para um vetor unitário temos:
Como sabemos que:
Substituindo o módulo unitário:
Ou seja:
E é isso pessoal. Espero que a resolução tenha sido proveitosa para todos. Até mais.
Resposta
Ver passo a passo.