O terceiro polinômio de Maclaurin de é
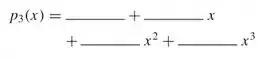
Passo 1
Essa questão é bem básica e aborda o conceito teórico de Polinômio de Maclaurin, tenho certeza que você, aluno do Responde Aí, vai conseguir resolver rapidinho.
Olha só, primeiro nós vamos relembrar a série de Maclaurin é um polinômio, que tem a condição de existência das derivadas sucessivas: f ’(0), f ’’(0), f ’’’(0), fn(0), ..., onde apresenta um processo de cálculo simplificado.
O polinômio de MacLaurin é um caso particular das séries de Taylor, quando x0 =0 , se obtém a seguinte série de MacLaurin:
![]()
Passo 2
Logo, primeiramente precisamos escrever até o terceiro polinômio de Maclaurin, assim:
Passo 3
E depois basta substitui na série, considerando:
Logo, a série tem os seguintes termos: