Mostre que
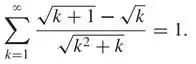
Passo 1
Essa questão é extremamente fácil de resolver pelo fato de o comando já informar tudo que nós precisamos saber, acredita?
Olha só, a equação dada é da soma de uma fórmula geral de uma série, o comando também pede para provarmos que para qualquer valor de k tendendo ao infinito teremos a resposta 1.
Passo 2
Arrumando a equação, temos:
E por fim, utilizando a propriedade de séries, basta aplicarmos o limite na Soma da equação e teremos o resultado esperado:
Viu com foi simples? Topa resolvermos mais uma questão juntos?
Resposta
Ei, a resposta está no passo a passo :)