Calcule a integral de superfície
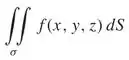
![]()
Passo 1
Topa resolver essa questão?
O primeiro passo para resolvermos essa questão é entender que a integral de superfície dada também pode ser escrita de outra forma, visto que:
Logo, podemos escrever:
Passo 2
Podemos parametrizar a equação z para obter o valor de dS, assim, se , logo:
Sabendo que , podemos considerar o plano z=1 e reescrever , substituindo na equação (1), temos que
Passo 3
Sabendo que R é a projeção de σ no plano xy, podemos reescrever a integral dupla obtida como uma integral iterada, desse modo
Aqui basta resolvermos da seguinte forma, , primeiro a integral de dentro (dr) e depois a de fora (dθ)