Associe cada equação diferencial com sua família de soluções.
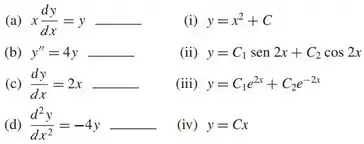
Passo 1
A forma mais fácil de resolver esta questão é usar o método de fatores integrantes nas alternativas de fácil resolução, no caso a) e c).
O primeiro passo para resolvermos essa questão é lembrarmos o método dos fatores integrantes que exige que a equação esteja na forma:
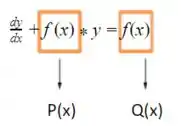
Assim, arrumando os termos e os dividindo por “x” e temos:
A partir disso é possível determinar os coeficientes P(x)= e Q(x)=.
Depois determina-se o fator integrante (u), sendo . Substituindo, temos:
→ →
E por último é só aplicar os valores obtidos na fórmula: . Portanto:
.
Isolando o “y” temos a solução iv):
Passo 2
c)
A letra c) é resolvida da mesma forma da a). Identifica-se que ela já está na forma adequada, então identifica-se P(x)=0 e Q(x)=2x
Depois determina-se o fator integrante (u), sendo . Substituindo, temos:
→ →
E por último é só aplicar os valores obtidos na fórmula: . Portanto:
.
Isolando o “y” e resolvendo a integral, temos a solução i):
Passo 3
Para resolvermos a letra b) e d) usaremos uma estratégia de associar ao seguinte modelo de equação geral: . Considerando ‘a’ e ‘b’ constantes, temos.
Escrevendo a equação na característica da equação geral:
Percebe-se que temos uma equação do segundo grau que gera raízes reais, assim, de acordo com a regra, o modelo da solução geral deve seguir o modelo:
Assim, resolvendo a equação (1) pela fórmula de Bhaskara temos a raiz=±2 , substituindo a raiz na equação (2), temos a equação geral iii) :
d)
Fazendo a mesma estratégia da letra b). Escrevemos a equação na característica da equação geral:
Percebe-se que temos uma equação do segundo grau que gera raízes imaginárias, assim, de acordo com a regra, o modelo da solução geral deve seguir o modelo:
Assim, resolvendo a equação (1) pela fórmula de Bhaskara temos a raiz=±2i , substituindo a raiz na equação (2), temos a equação geral ii) :
Resposta
a) →
b) →
c) →
d) →