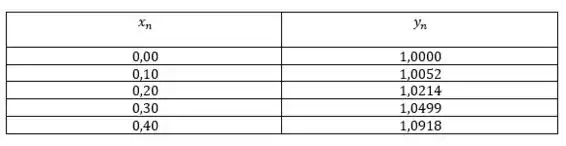
Com auxílio do método de Milne, obtenha uma aproximação do valor de , onde é a solução do problema de valor inicial do exemplo 1. Tome e aplique o método de Runge-Kutta para calcular
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão ele pede para achar método de Adams-Bashforth/Adam-Moulton e o método de runge-kutta para,
Lembrando que para essa questão temos que usar a fórmula do método Adams-Bashforth/Adam-Moulton em que,
Para
E o método Milne é formada por,

Passo 2
Sabendo que,
, usando
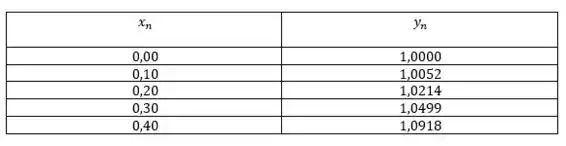
Prontinho é isso, até a próxima meu camarada.

Resposta