Um avião desloca-se em voo horizontal, 8 milhas acima do solo (Supor que a terra é plana). A rota do voo passa sobre um ponto P do solo. A distância entre o avião e o ponto P decresce na razão de 4 milhas por minuto, no instante em que essa distância é de 10 milhas. Determinar a velocidade do avião em milhas por hora.
Passo 1
Vamos criar uma figura que nos ajude a entender o que está ocorrendo
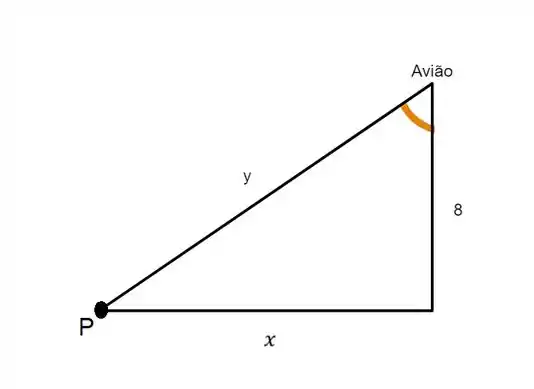
Temos que o segmento de reta com tamanho x é nossa “terra plana”, enquanto a altura é a altura do avião acima do solo (8 milhas) e y é nossa distância entre P e o avião.
Vale lembrar que a derivada da posição pelo tempo nos da a velocidade pelo tempo, usaremos isso.
Passo 2
Perceba a informação dada “A distância entre o avião e o ponto P decresce na razão de 4 milhas por minuto, no instante em que essa distância é de 10 milhas.” Isso quer nos dizer, de forma mais direta, que a derivada da (posição em relação à P), em função do tempo é de 4 milhas por minuto, quando temos y = 10 milhas, ou seja, a velocidade do avião em relação à P é de 4 milhas por minuto = 240 milhas por hora.
Em termos matemáticos:
Passo 3
Porém, a questão nos pede a velocidade horizontal do avião que seria meio que a “velocidade real”.
Como nós queremos (V horizontal) porém só temos informação de , vamos achar uma forma de relacionar x e y.
Veja pela nossa figura que temos um triangulo retângulo, que vale Pitágoras.
Derivando em y: