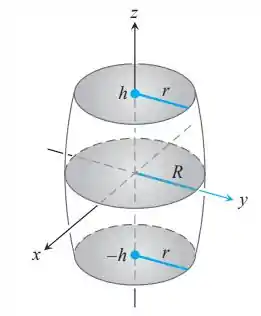
O barril mostrado aqui tem o formato de um elipsoide com partes iguais cortadas a partir das extremidades por planos perpendiculares ao eixo z. As seções transversais perpendiculares ao eixo z são circulares. O barril tem 2h unidades de altura, o raio de sua seção média é R e os raios de suas extremidades são ambos r. Encontre uma fórmula para o volume do barril. Em seguida, verifique dois pontos. Primeiro, suponha que os lados do barril sejam endireitados para torná-lo um cilindro de raio R e altura 2h. Sua fórmula fornece o volume do cilindro? Em segundo lugar, suponha que r = 0 e h = R, de forma que o barril seja uma esfera. Sua fórmula fornece o volume da esfera?
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de vetores e geometria espacial.
Vamos agora resolver os exercícios da seção 6 sobre cilindros e superfícies quádricas.
A partir do enunciado temos que o elipsóide tem a forma:
Para determinarmos c2, notamos que o ponto (0, r, h) está na superfície do barril.
Então:
O volume é calculado por:
Sendo:
Passo 2
Se r = R, teremos que:
Que é o volume de um cilindro de raio R e altura 2h.
E se r = 0 e h = R:
Que é o volume de uma esfera de raio R.
E é isso pessoal. Espero que a resolução tenha sido proveitosa para todos. Até mais.
Resposta
Ver passo a passo.