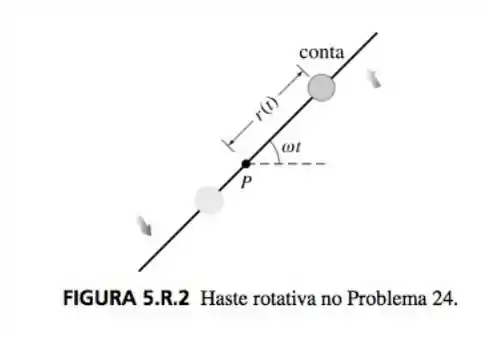
Uma bolinha furada desliza ao longo de uma barra de comprimento L. A barra está girando em plano vertical a uma velocidade angular constante em torno de um pino P fico no ponto médio da barra, mas a forma do pino permite que se movimente ao longo de toda a barra. Seja a posição da bolinha furada relativa ao eixo de coordenadas que está girando, como mostra a figura 5.R.2. Para aplicar a segunda lei de Newton a esse sistema de referência móvel, é necessário usar o fato de que a força resultante que age sobre a bolinha é a soma da força real (nesse caso, a força da gravidade) e as forças inerciais (de Coriolis, transversal e centrifuga). A matemática é um pouco complicada, vamos somente dar a equação diferencial resultante para :
- Resolva equação diferencial sujeita às condições iniciais
- Determine as condições iniciais para as quais a bolinha exibe um movimento harmônico simples. Qual é o comprimento mínimo L da barra que pode ser conciliado com um movimento harmônico simples da bolinha?
- Para condições iniciais diferentes das que foram obtidas no item b), a bolinha cedo ou tarde voará para fora da barra. Explique, usando a solução do item a)
- Suponha que o comprimento da barra seja para cada par de condições iniciais do item d), use um aplicativo que determina raízes para encontrar o tempo total que a bolinha permanece na barra.
Passo 1
Faaaala, cara! Tranquileba?
Temos que:
Passo 2
Sabemos que uma equação diferencial linear, não homogênea de coeficientes constantes e de segunda ordem, admite como solução geral é a soma da solução transiente com a solução estacionário Sendo, portanto
Para
Façamos
Logo:
Onde e são definidos pelas condições iniciais.
Logo
E
E:
Logo:
Passo 3
Para
Sabemos que em um espaço vetorial de dimensão 2, existem infinitos vetores linearmente independentes, assim criemos uma função participante do mesmo espaço vetorial. Então
De forma que podemos fazer uma função
Façamos
Logo:
E portanto:
Ou