Se C for uma curva lisa por partes de (1, 2, 3) a (4, 5, 6), então
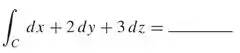
Passo 1
Antes de começar a resolver a questão, nós temos que relembrar que o integrando da integral pode ser expresso como F · dr, onde F é o campo vetorial. Assim, podemos escrever a integral como:
Passo 2
O símbolo 𝜙 representa a Função Potencial, para obtermos ela, iremos individualmente fazer uma derivada parcial e integrar a função dada
Os termos , e surgiram porque fizemos derivadas parciais, até aí tudo certo né? Mas como vamos relacionar o resultado das três integrais, tem alguma possibilidade de termos F(x,y,x) = x + 2y + 3z + ... ?
Simmm, isso porque nós temos os termos A, B e C desconhecidos.
E por fim, temos que colocar a constante K de integração, logo:
Passo 3
O último passo é substituir 𝜙 na equação (1), considerando () = (4, 5, 6) e () = (1, 2, 3), temos:
Viu como foi fácil? Topa resolver mais uma questão?
Resposta
18