Em cada parte, encontre a fórmula para o termo geral da sequência, começando com n = 1.
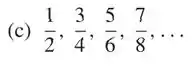
Passo 1
Mais uma questão facinha de resolver, acredita?
A ideia é analisar de modo bem lógico a forma a qual a sequência dos termos ocorre e criar hipótese de possíveis formas a qual o valor varia.
Passo 2
Analisando individualmente o número dos termos, percebemos que cada novo valor é somado a duas unidades, mas de que forma isso seria possível? Considerando que o numerador do é 1, teríamos que ter um valor fosse subtraído, concorda que se considerarmos o numerador como , temos: 2(1)-1=1 , 2(2)-1=3, 2(3)-1=7 e assim por diante.
Passo 3
Na parte do denominador, o valor só é dobrado mesmo, então, facilmente pensamos em . Assim temos a seguinte equação geral da sequência:
Vamos testar nossas suposições: