Em cada um dos Problemas de e dada uma função em um intervalo
a) Esboce os gráficos das extensões periódicas par e ímpar de períodos da função dada em um intervalo de três períodos.
b) Encontre as series de Fourier em cossenos e em senos da função dada.
c) Faça os gráficos de algumas das somas parciais de cada serie.
d) Para cada serie. Investigue a dependência em n do erro máxima em
Passo 1
Saudações galerinha! Tudo bem?
Vamos juntos resolver esse longo exercício?
Inicialmente vamos lembrar que:
Se é uma função par, então a série de Fourier de coincide com a série de Fourier em cosseno:
Se é uma função ímpar, então a série de Fourier de coincide com a série de Fourier em seno:
Para plotar nossa extensão periódica par de f com L= 1 , temos que :
Nosso gráfico ficará assim:
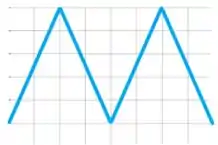
Variando os eixos de e
Para plotar nossa extensão periódica ímpar de com L= 1 , temos que :
Nosso gráfico ficará assim:
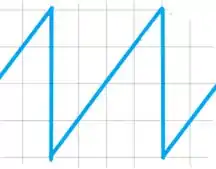
Variando os eixos de e
Passo 2
Neste item vamos encontrar a série de Fourier par e impar para a função dada. Beleza!
Para expansão Par teremos:
Ou
Para expansão ímpar teremos:
Ou
Passo 3
Neste item vamos plotar algumas partes das somas parcial das séries encontrada. Tranquilo!
Para a expansão Par g(x) teremos:
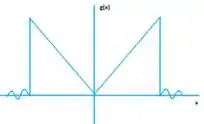
Para a expansão ímpar h(x) teremos:
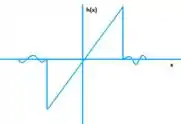
Até aí tranquilo?

Passo 4
Quase acabando. UFA!
O erro máximo não se aproxima de zero em nenhum dos casos, devido ao fenômeno de Gibb. Observe que os coeficientes ambas as séries se comportam como quando já que existe um no numerador.
Prontinho!
Te vejo na próxima questão!
Resposta
Par
Ímpar