Uma caixa aberta foi construída com um retângulo de cartão, retirando quadrados iguais em cada vértice e dobrando para cima os lados. Achar as dimensões da caixa de maior volume que pode construir-se deste modo se o retângulo tem lados (a) 10 e 10; (b) 12 e 18.
Passo 1
Fala ae, blz?
Para a letra a), vamos desenhar a situação retirando os quadrados dos vértices.
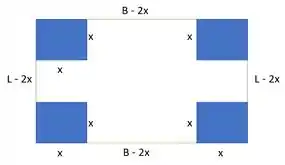
Assim, pelo enunciado temos que L = B = 10.
O cálculo do volume da caixa será:
Passo 2
Para acharmos o Volume máximo, basta derivarmos e igualarmos a zero:
Derivando:
Igualando a zero para acharmos os pontos críticos:
Como a caixa tem lado 10 – 2x, quando x = 5 teremos o volume mínimo (zero), e quando x = 5/3 teremos o volume máximo.
Logo, a dimensão da caixa nesse caso será:
Passo 3
Para a letra b) o desenho é o mesmo, só muda as dimensões:
L = 12 e B = 18.
O cálculo do volume da caixa será:
Passo 4
Para acharmos o Volume máximo, basta derivarmos e igualarmos a zero:
Derivando:
Igualando a zero para acharmos os pontos críticos:
Como a caixa tem um lado 12 – 2x, quando teremos um volume negativo, o que não faz sentido, portanto, quando teremos o volume máximo.
Logo, a dimensão da caixa nesse caso será:
Resposta
a)
b)