Calcule o comprimento do astróide (Figura 11).
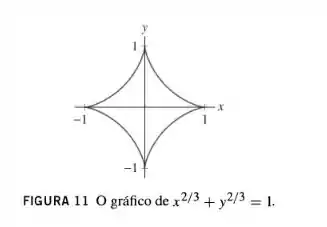
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Primeiramente, vamos calcular a derivada de
Portanto, trabalhando com nós temos que
Desenvolvendo um pouco mais os termos, nós temos que
Passo 2
Calculando o comprimento de arco no primeiro quadrante, nós obtemos o seguinte resultado
Desenvolvendo
Que tem como resultado
O arco total é igual a