Calcule e interprete geometricamente o resultado obtido
Letra a)
Onde é a coroa circular
Com
Passo 1
O problema sugere uma integral de superfície e a superfície é a seguinte coroa circular
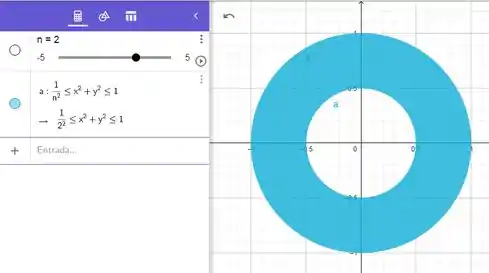
Passo 2
Se ao invés de resolvermos esta integral em coordenadas cartesianas, resolvermos em coordenadas polares o trabalho será deveras abreviado
Podemos trabalhar em termos do ângulo teta () e dos raios () das circunferências que compõem a coros, ou seja
varia de até , ou seja varre todo o plano
Para a restrição , só sabemos que é maior ou igual a
E como agora estamos trabalhando com e os diferenciais não serão mais e sim
Passo 3
Tirando a raiz quadrada da restrição teremos
E . Aplicando ao limite vamos obter
A raiz quadrada do integrando é o próprio
Obtendo
A primeira integral tem como resultado implicando em
O resultado de
Dessa forma