O campo de direção para d/dx = 4x/y aparece na Figura 1.13.
- Verifique se as linhas retas são curvas de solução, desde que .
- Esboce a curva-solução com condição inicial y(0) = 2
- Esboce a curva-solução com condição inicial y(2) = 1
- o que você pode dizer sobre o comportamento das soluções anteriores quando ? E quando ?
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
- Sejam as linhas y=±2x. Como dxdy=±2 então:
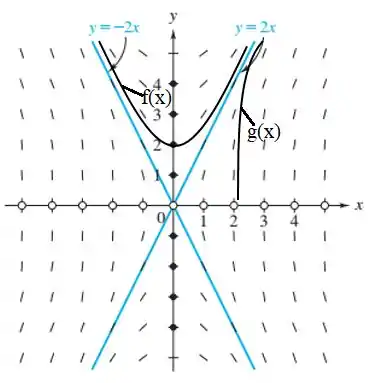
- O gráfico da solução da equação diferencial que passa pelo ponto (0,2) deve ter inclinação neste ponto. Então, para traçar a curva solução f(x) satisfazendo a condição y(0)=2, poderíamos passar para uma curva adjacente.
- O gráfico da solução da equação diferencial que passa pelo ponto (1,2) deve ter inclinação neste ponto. Então, para traçar a curva solução g(x) satisfazendo a condição y(1)=2 podemos passar para uma curva adjacente. As curvas de solução são mostradas na figura a seguir.
- As curvas de solução tornam-se infinitas quando x→∞ e têm a linha y=2 como assíntota. A curva solução da parte (a) torna-se infinita e tem a linha y=−2 como assíntota quando x→−∞. A curva de solução da parte (b) não existe para x negativo.
Assim, as linhas y=±2x são curvas solução da equação diferencial dada.
Passo 2
Passo 3
Resposta
Resposta nos passos.