O campo de direção para dy/dx = 2x + y aparece na Figura 1.12.
- Esboce a curva-solução que passa por (0, -2). Por esse esboço, escreva a equação para a solução.
- Esboce a curva-solução que passa por (-1,3).
- O que você pode dizer sobre a solução no item (b) quando ? E quando ?
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
Requerido: Para a equação Esboce a curva solução que passa pelos pontos dados e encontre o comportamento assintótico.
a) Esboce a solução que passa por (0,-2) e dê sua equação. Podemos ver que se começarmos no ponto (0,-2) e seguirmos as linhas de inclinação, continuaremos ao longo de uma linha reta . Portanto, nossa curva de solução é uma linha reta.
Reorganizando a equação na forma e comparando-a com a equação da reta (y= mx+c, c é a interseção em y e m é a inclinação constante) nos diz que a equação para nossa linha reta é:
onde no ponto dado
Também podemos encontrar o valor da interceptação y( de y(0)=−2y, dando-nos −2=c−2∗0 então c=−2, a partir disso abordagem também.
O gráfico é dado como:
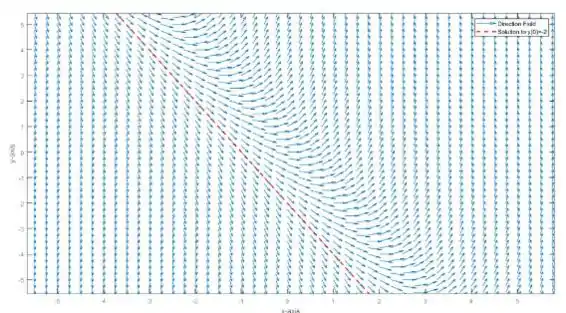
Passo 2
b)Esboce a solução que passa por (-1,3) e dê sua equação .\par Começando no ponto (-1,3) e traçando as inclinações obtemos o seguinte gráfico:
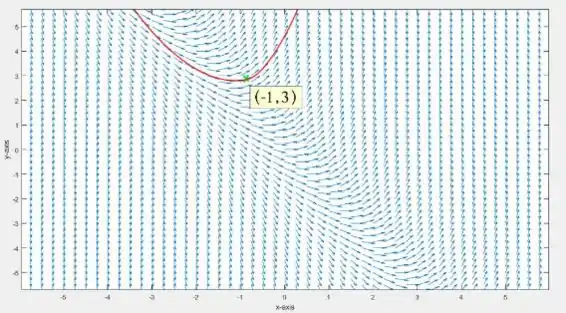
Passo 3
c) c) Determine o comportamento assintótico. A partir dos dois gráficos, fica claro que y deve se aproximar de ∞ para x para −∞ e x para +∞.
Resposta
Os esboços para diferentes condições iniciais são fornecidos.