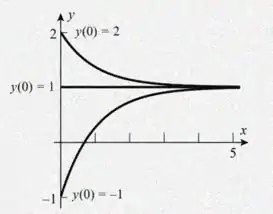
Um campo de direções para a equação diferencial y’ = 1 − y está mostrado na figura em anexo. Em cada parte, esboce o gráfico da solução que satisfaz a condição inicial.
(a) y(0) = −1
(b) y(0) = 1
(c) y(0) = 2
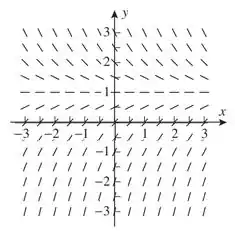
Passo 1
Fala galera, essa questão é moleza de entender, acredita?
Olha só, a primeira coisa que nós temos que saber é que o valor da tangente de y’ na equação representa a inclinação do campo de direções.
Passo 2
Sabendo disso, nós começamos fazendo as análises substituindo os valores indicados na equação fornecida, assim temos:
- Se y(0) = -1
- Se y(0) = 1
- Se y(0) = 2
Passo 3
Esses valores obtido significam que quando x=0, a depender do valor que corta o eixo ”y” temos um “ y’ “, sendo y’ = tan(θ). Essas informações armazenadas geram o seguinte gráfico
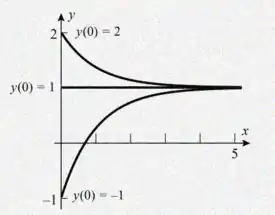
Resposta