Quando uma carga P é aplicada a uma longa coluna delgada de seção transversa uniforme e comprimento L, a coordenada de um ponto de sua curva de deflexão é dada por
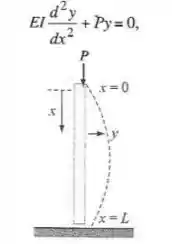
Onde as constantes são respectivamente, o módulo de elasticidade de Young e o momento de inércia da seção transversa. Se a coluna é impedida de rotar em seu topo e em sua base, as condições de contorno são .
a) mostre que esse problema de valores no contorno indica que a coluna não verga, a menos que a carga P tenha um dos valores essas diferentes cargas são chamadas cargas críticas.
b) mostre que a curva de deflexão correspondente à mais baixa carga crítica chamada carga Euler, é Então é chamado primeiro modo de deformação
Passo 1
Falaaaaa rapaziada tudo blz?
Nesta questão ele pede para determinarmos que
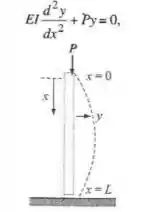
Ele pede para determinarmos,
a) mostre que esse problema de valores no contorno indica que a coluna não verga, a menos que a carga P tenha um dos valores essas diferentes cargas são chamadas cargas críticas.
b) mostre que a curva de deflexão correspondente à mais baixa carga crítica chamada carga Euler, é Então é chamado primeiro modo de deformação

Passo 2
Na letra (a) sabendo que
Para mostrarmos que esse valor no contorno fica
Passo 3
Na letra (b) para mostrarmos que, tendo,
Derivando a função temos

Gostou meus abençoados? espero ter ajudado.
Resposta