Classifique a série como absolutamente convergente, condicionalmente convergente ou divergente.
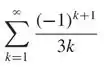
Passo 1
E aí, aluno do Responde Aí!!
Para essa questão vamos primeiro lembrar que uma série é absolutamente convergente se a série de valores absolutos for convergente. E uma série é condicionalmente convergente se a série de valores absolutos diverge, mas a série converge. E, caso contrário, a série é divergente. Então, vamos começar por testar a convergência absoluta.
Passo 2
Um teste que pode ser facilmente aplicado é o teste da Comparação, nesse caso temos de ter uma série “mais simples”, mas que tenha uma certa semelhança à série da questão, logo, concorda que podemos utilizar?
Sabendo que a série (1) diverge, a série dada na questão também diverge pelo teste da comparação.
Passo 3
Para validarmos se a série é realmente divergente, aplicamos um segundo teste, desta vez, usaremos o Teste da Séries Alternadas, uma vez que a série tem o número negativo elevado à um expoente variável, .
Nesse teste, vamos avaliar que a sequência é convergente se a série satisfaz dois critérios:
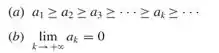
- Se:
- E também:
Logo, temos uma série que converge pelo Teste das séries Alternadas.
Como cada teste teve uma resposta diferente, podemos dizer que a série é condicionalmente convergente.
Resposta
Condicionalmente convergente