Considere a equação diferencial
para a população p(em milhares) de uma certa espécie no instante t.
(a) Esboce o campo de direção usando ou um software de computador ou o método das isóclinas.
(b) Se a população inicial é 4.000 [ou seja, p(0) = 4], o que você pode dizer sobre a população limitante limt → + ∞ p(t)?
(c) Se p(0) = 1,7, o que é limt → + ∞ p(t)?
(d) Se p(0) = 0,8, o que é limt → + ∞ p(t)?
(e) Uma população de 900 pode aumentar para 1.100?
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
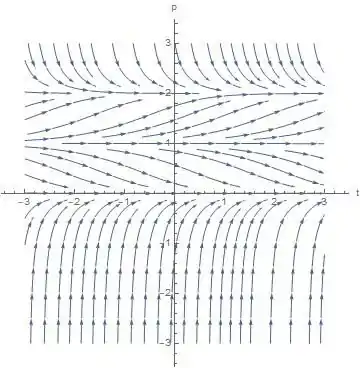
- O gráfico do campo de direção é:
- A partir do campo de direção, podemos ver que todas as curvas de solução com p(0)>1 chegarão perto da assíntota horizontal p(t)=2 como t→∞. Portanto
- A partir do campo de direção, podemos ver que quando 1
onde .
Passo 3
- A partir do campo de direção, podemos ver que quando 0≤p(0)
onde
- Do campo de direção podemos ver que p(t)=1 é uma assíntota. Também podemos ver que quando p(0)=0,9 todas as curvas de solução chegarão perto de zero quando t→∞. Em outras palavras, a população de 900 diminui com o tempo. Portanto, a população de 900 não pode aumentar para 1100
Passo 2
onde .
Resposta
Resposta nos passos.